Notes: A task based on this image appears in the excellent book, Extending the Challenge in Mathematics, by Linda Jensen Sheffield, published by Corwin Press in 2003. See her book for a detailed discussion that includes examples of students' thinking. The problem is similar to the Triangle Sums activity but works especially well for younger students.

Tasks and questions: Insert a different number into each square so that the sum of the bottom row equals the sum of the left column. How many solutions are possible? Does every solution make the same sum?  What sums are possible? Are there patterns in the sums? Which numbers can be in the corner? Why does the corner have to be an odd number? What would happen if there were an extra square in each row and column and I use the numbers 1 through 7? Would it still make a solution if I added 1 to each number? What would the new sum be? Would the corner still have to be an odd number? Why or why not? Would it still make a solution if I doubled each number? What would the new solution be? What would happen if I kept subtracting 1 from the numbers in one of my solutions? Can negative numbers, fractions, or decimals be use in the puzzle? What happens if you multiply the numbers instead of add them?

Keep asking new questions!

Notes: Those who are familiar with "frames and arrows" problems may have seen this type of set-up. Encourage students who are new to multiplication and division to create their own strategies for handling large numbers or fractions. You could also redesign the problem to use addition and subtraction instead. The questions at the end will help older or more advanced students to explore properties of exponents.

Tasks and questions: Use only x 4 and ÷ 8 to change 64 into 2 in five steps. Write numbers in the other circles to show your answer at each step. Is there more than one solution to the problem? Do the solutions have anything in common? How many solutions are there? How can I be sure when I have found all of the solutions? Do the numbers in the solutions always have to even? Why or why not? Can the solutions contain fractions? Decimals? Negative numbers? What happens if I change the number of circles? Can I do the problem backwards (turning 2 into 64)? Can I use my original solutions to help me find "backwards" solutions? Why does this work? What happens if I use ÷ 4 and x 8 instead? Are there still solutions? What happens if I use x 3 for one of the choices? How many solutions are there now? Can I create problems like this that have no solution? Can I create problems like this that have more solutions than this one? What happens if I write all of my numbers in exponential form? (Suggestion: Use the number 2 for a base.) Do the exponents help me think of new solution strategies? Is it possible to write the fractions in exponential form, too? How do these exponents relate to my new solution strategies? Can I the use the idea of exponential form to create new problems that have exactly the same number of solutions as this one? Can I use the idea of exponents to help me create an addition / subtraction problem like this for every multiplication / division problem? 

Keep asking new questions!

Notes: This problem is great for students who are just beginning to learn about area (before they learn formulas for it) or for students who know formulas but could benefit from getting a deeper understanding of the meaning of area.

Tasks and questions: Create more polygons that have the same area as these polygons. How many polygons can I find? Is it okay to join squares on the grid at their corners (vertices) instead of along a side? Can I make solutions that look like things in the real world or my imagination? How many solutions can I make from whole squares on the grid? Does it count as a new solution if I reflect (flip) or rotate (turn) an old solution? How many solutions can I make from half-squares and whole squares?  How many ways are there to make the half-squares that I use to build my polygons? Can I make solutions that use smaller parts of the square units? How small? What happens to the area when I join two of my polygons? Does it matter how I join them? Why? How many triangles can I make that have an area of 4 square units? Quadrilaterals? Pentagons? etc. Can I use patterns to find new solutions? How many solutions are there all together? Do all of my polygons have the same perimeter? What kinds polygons have smaller perimeters? Larger perimeters? What happens to the perimeter when I join two of my polygons? Does it matter how I join them? 

Keep asking new questions!

Notes: This problem relates to points on a grid (called lattice points) that lie on a polygon (boundary points) and points that are inside the polygon (interior points). You create the sides of the polygons by connecting lattice points with line segments.

Tasks and questions: What is special about the large black dots? What it special about the open dots? How many boundary points does the polygon have? How many interior points does the polygon have? Can I make more polygons that have same number of boundary and interior points? When a point is very close to the side of a polygon, how can I be sure whether or not it is a boundary point? What is the smallest number of boundary points that a polygon can have? What is the smallest number of interior points that a polygon can have? Can I make a polygon that has the smallest possible number of both boundary and interior points? How many polygons like this can I make? Do they have anything else in common? Is it possible to create polygons with every possible combination of boundary and interior points (greater than the minimum)? Are there patterns in creating these polygons? Are there patterns in the appearances of the polygons? What are the areas my polygons? What happens to the number of boundary points, interior points, and area when I move one vertex of a polygon one lattice point to the horizontally or vertically? Or both? Are these changes predictable or do they depend on the details of the shape? Is it possible to predict the area of a polygon using the number of boundary points and interior points?

Keep asking new questions!

Notes: This problem comes from the book Advanced Common Core Math Explorations: Numbers and Operations, Prufrock Press, 2015 and is used by permission. It is about an imaginary planet called Torr whose inhabitants group by fours instead of tens for their place value, which changes the way they write their numerals. 

Tasks and questions: The inhabitants of the planet Torr have two fingers on each hand. Figure out how the Torrans write their numerals. What is the value of each place in the Torran place value system? What are the patterns in these values and what causes them? Can I discover fast ways to convert one of our numerals into a Torran numeral? Can I discover fast ways to convert a Torran numeral into one of our numerals? Why is the number nineteen written as a three-digit numeral in the Torran system? What would Torran place value blocks look like? (Think of the "base 10" blocks that our students use to learn about place value.) Do the Torran numerals ever have a digit greater than 3? Why or why not? Are there patterns in the ways that the Torrans count? What would the Torran algorithms for addition, subtraction, multiplication, and division look like? Would these Torran calculations be easier or harder to learn than ours? Why? Would Torrans have anything like our "decimals"? How would these work? Would our repeating decimals always be repeating for them? Would their prime numbers be the same as our prime numbers? Would they look the same when I write them down? What if there were another culture on Torr that grouped by eights instead of fours? How would I answer all of these questions for them? Would there be a quick way to translate between the numeration systems of these two cultures (without using our system at all)? How long is a Torran day? A Torran year? How might Torrans measure these types of things?

Keep asking new questions!

Notes: How can a simple statement like this be the seed for a problem that never ends? Think about it for a while before reading further. One possibility is that it could inspire students to construct their own measurement system, a creative task that can take them in many new and exciting directions!

Tasks and questions: How long is 1 akonid? If ako- is a prefix, what could it mean? How many nids are in an akonid (or how many akonids are in a nid?) How many akonids (nids) tall am I? How many nids and akonids are in one foot? In one mile? How many feet are in an akonid (nid)? How long is 1 million akonids (nids)? How about 1 billion or 1 trillion akonids (nids)? How can I measure lengths in nids and akonids without thinking about familiar units like inches or feet? How could I create a nid ruler to make measurements? Does it matter what materials I use? If I made a lot of these rulers, how could I be sure that they were all accurate (consistent with each other)? What other prefixes could I use for nids? What should each prefix stand for (and are some choices better than others)? How might the Torrans (see above) subdivide a nid ruler? Would they do it differently than we would? What would a square nid and a cubic nid look like? How could I measure them? What is the area of my classroom floor in square nids? What is the volume of my classroom in cubic nids? What things do I know that would measure about 1 million square (or cubic) nids? How much does one cubic nid of water weigh? If I made up a name for that weight, could I use it to measure other weights? Would it be practical to use something other than water for this purpose? Why or why not? Can I figure out how much my math book weighs using my new unit of weight? Can I use the same prefixes for my weight measurement that I used for my length measurements? Could I create a new unit for measuring time? How would I measure it without referring to familiar units such as seconds?

Keep asking new questions!

Notes: This list of fractions comes from the book Advanced Common Core Math Explorations: Ratios, Proportions, and Similarity. Prufrock Press, 2016 and is used by permission. The list can be extended forever, but in ways that you might not expect! It is the basis of an excellent activity for students who are learning about comparing fractions, but there is much more to it than meets the eye. Professional mathematicians are still discovering new things about these ideas!

Tasks and questions: There seem to be many addition or subtraction equations with the numerators and denominators of these fractions. Why does this happen? Why are the smallest numerators and denominators in the left and right fractions? Why are the largest numerators and denominators in the second and fourth fractions? What pattern was used to create the list? Can I use the pattern to extend the list to the left and/or right? Can I use the patterns to extend the list in other ways? How long can I make the list? Why are all of the fractions in simplest form? Are all of the fractions still in simplest form when I extend the list? Why or why not? What happens if I arrange the fractions in order of size? I wonder why the fractions always increase from left to right when I extend the list? Do the fractions increase at a constant rate? Do they increase according to some other pattern? What happens to the list if I start with new fractions on the left and right? What happens to the list if I begin with the greater fraction on the left? What happens to the list if I begin with fractions that are not in simplest form? What happens to the list if I begin with two equivalent fractions? Is it possible to find two numbers to start with so that every possible fraction eventually appears in the list when I extend it? Or does this already happen with the list we began with? What would happen if I used multiplication (or another operation) on the numerators and denominators to create the fractions in between?

Keep asking new questions!

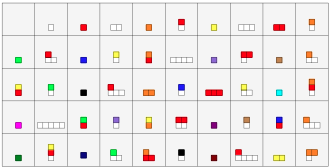
Notes: This image comes from Advanced Common Core Math Explorations: Factors and Multiples, Prufrock Press, 2014 and is used by permission. It is a personal favorite of mine. I like to use it at the beginning of the school year with upper-elementary / middle school students. After we figure out what the grid is about, we use it all year long. By the way, this is a great problem for adults, too! See Math Building Blocks to learn more.

Tasks and questions: What patterns do you see? Do you see anything related to rows, columns, or diagonals?  What happens in the cells that have only white blocks? What about the ones with only red blocks? How can I predict the next cell that contains a red block? How can I predict the next cell that contains at least two white blocks? How can I predict the next appearance of other combinations of colors? Is it possible to continue the grid downward? How long will the grid continue? Why is the upper left cell blank?  What happens if I number each cell (left to right, top to bottom as you would read a book)? If I do this, should I start with 1 or 0? Why? is there a pattern to how the blocks are arranged within each cell? Is this pattern important from a mathematical standpoint? If I continue the grid, will every new cell have blocks in it? Will every cell have its own unique collection of blocks? Will every possible combination of blocks occur in some cell? What patterns can I find in the number of white blocks in each cell? The number of red blocks in each cell? Other colors? How are all of these patterns related to each other?

Keep asking new questions!

Notes: This image is intended to bring out questions about angles in polygons. However, if your students come up with other ideas, be sure to follow up on them!

Tasks and questions: What is different about how the two hexagons are decomposed into triangles? What would it look like if you decomposed triangles, quadrilaterals, pentagons, heptagons, etc. into triangles in the same ways? How does the number of sides relate to the number of triangles for each way of decomposing polygons? Why does this happen? Can you write algebraic expressions or formulas for these relationships? How can each picture help you find information about the (interior) angles in the hexagons (and other polygons)? What kind of information? What process does each image suggest for finding the sum of the angles in a polygon? Can you write these processes as algebraic expressions or formulas? Do your two formulas always give the same answer for polygons with the same number of sides? Why or why not? Are there other ways of subdividing the polygons into triangles that give even more processes and formulas for finding the sums of angles in polygons?  How do these formulas relate to each other? What patterns do you see in them? How can you prove that they are all equivalent? Can you draw the same kinds of pictures for concave polygons? Can the formulas that you discovered be used for concave polygons? How do you know?

Keep asking new questions!

Notes: Sometimes, even the most familiar pictures can lead to can lead to great problems that never end—simply by paying close attention to the details as you play with the ideas. This problem comes from Advanced Common Core Math Explorations: Measurement and Polygons,  Prufrock Press, 2014 and is used by permission.

Tasks and questions: How can I find the measures of the angles at the tips of the stars by using what I know about the angles in the pentagon? How many different strategies can I find for doing this? Notice how the star is formed by extending the sides of a regular pentagon. Create new stars by extending the sides of other regular polygons. What are their star-tips angles? Are there patterns in the sizes of the star-tip angles of stars formed from different regular polygons? Can I write an algebraic formula or expression relating the number of sides in the polygons to the star-tip angles? Is there more than one formula? How does each formula relate to a different strategy or a different way of thinking about the star-tip angles? Can I use algebra to prove that these formulas are equivalent? What happens if I try to use the formula for a triangle or quadrilateral? How does this relate to what happens when I try to create a star from these polygons? What happens to the star-tip angles as the number of sides keeps increasing? How can I understand this using a formula? A table? The pictures of the stars? What are the sums of the star-tip angles in a star? What patterns are there in these sums? How do these patterns relate to the sums of the interior angles in the original polygons? Why do some polygons create multiple layers of stars when I extend their sides? How can I quickly predict the number of layers? What are the patterns in the angles for the star-tips of the different layers? Can I create a single formula that calculates the star-tip angle for any layer of any star? Is it possible to create stars from polygons that are not regular? Is there a quick way to predict which polygons will create complete stars? Are there formulas these star-tip angles or their sums?

Keep asking new questions!