Back to Creative Math Prompts          Previous prompt for middle grades          Next prompt for middle grades
 

Thought for the day: Inserting blank spaces into a multiplication table encourages students to predict products of fractions or decimals before they learn the rules.

Concepts: multiplying decimals and/or fractions; patterns in multiplication (possibly division)

Beginning

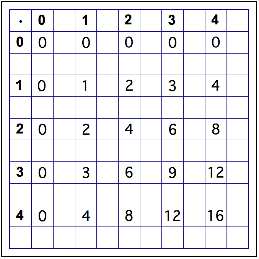
I notice that this multiplication table includes 0.
I notice rows and columns inserted between each row and column in a regular multiplication table.
I notice that the entries shown in the table match the ones in a regular multiplication table.
I notice that the whole numbers in each row (column) increase by the amount of the first whole in the row (column).
I wonder if the pattern of increasing by the same amount will continue when I fill in the blank cells.
I notice that the blank cells will probably have to include fractions (or mixed numbers) or decimals.

Exploring
I wonder how I can figure out the missing numbers that belong in the table.
I wonder if some of the new squares will contain numbers less than 1.
I notice that if I make all of the numbers in a row (or column) increase at a steady rate, the whole numbers still fit the pattern correctly.
I wonder if I can find other patterns to help me fill in the missing squares.
I wonder if I could create a table with even more rows and columns between each of the whole numbers.
I wonder if I can discover any shortcuts for multiplying fractions or mixed numbers.
I wonder if I could see new patterns by writing the fractions and mixed numbers as decimals.

Creating

As they notice and wonder, students may finish creating and exploring this table and others like it. Many of their creations may flow out of things that they have wondered about. For example, they may

Discover patterns that help them finish creating this table.
Create multiplication tables that show decimals instead of fractions and mixed numbers.
Create new multiplication tables by inserting more rows and column between the whole numbers.
Create multiplication tables that include negative numbers.
Try to create multiplication tables that include numbers like π.

Reflecting and Extending

I notice that I can multiply the fractions in the table without knowing any rules for multiplying fractions (using just patterns instead)!
I wonder if I could create multiplication tables to help me multiply any two fractions or mixed numbers.
I wonder if I could extend the table to include negative numbers.
I wonder if I could extend the table to include (irrational) numbers like π or the square root of 2.

Notes

This prompt guides students to think about the why behind multiplying fractions and/or decimals.

The idea—though it may take some time to get there—is for students to predict how to complete the table before you teach them rules for doing the calculations. For example, they may predict that the "1/2" row (or column) starts at 0 and increases by 1/2 every other square. When they fill in the intermediate squares, they discover that they need to count by 1/4s in order to make the numbers in the row increase steadily.

Even (or especially) if some students use patterns to complete the table fairly quickly, be sure that they step back and pay attention to what is happening. For example, they may be able to explain why it makes sense that 1/2 • 1/2 = 1/4 (because 1/4 is half of one-half) or why 3 1/2 • 1  1/2 should equal 5 1/4 (because it is 3 1/2 plus another half of 3 1/2).

Back to Creative Math Prompts          Previous prompt for middle grades          Next prompt for middle grades