Back to Creative Math Prompts Previous prompt for Later Grades Next prompt for Later Grades
Thought for the day: The examples and notes on these pages are suggestions. As much as possible, allow students to create the questions that lead to the problems they solve.
Concepts: adding, subtracting, multiplying, and factoring polynomials, polygonal numbers
Examples of noticing and wondering
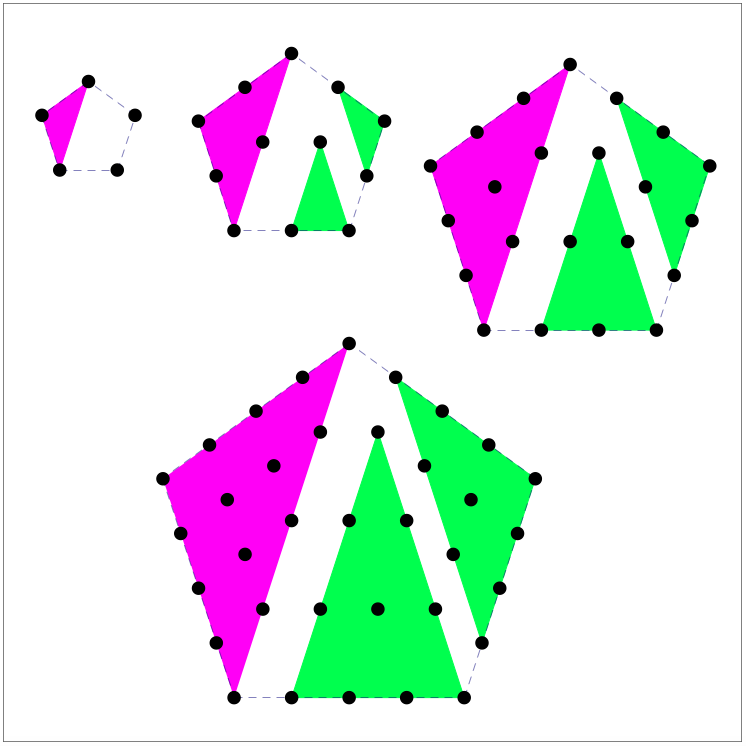
I notice four pentagons decomposed into triangles (one magenta and two green).
i notice that the magenta triangles are larger than the green ones with each pentagon.
I notice that the two green triangles within each pentagon have the same number of dots.
I notice patterns in the number of dots within each triangle.
I notice that you can count dots within the triangles by adding consecutive natural numbers (1 + 2 + 3, etc.)
I wonder if the patterns will continue when I make larger pentagons.
I wonder if there is a pattern to the total number of dots within each pentagon.
I wonder if I can use the triangles to help count the dots in the pentagons more quickly.
I wonder if I can use the triangles to create a formula for counting the dots in the pentagons.
I wonder if I can discover patterns like these for other polygons.
Creating something new
Students can:
Create pictures like these for larger and larger pentagons.
Try to create different arrangements of triangles within them or to decompose in entirely different ways.
Draw pictures like these for other types of polygons.
Discover/create as many patterns as they can.
Create a formula for each pattern they discover.
Join formulas together into more general "master" formulas.
Notes
See the Polygon Polynomials exploration on the Deep Algebra Projects page of this website for a more structured activity that delves deeply into concepts related to this prompt.
The green triangles represent the triangular numbers, 1, 1 + 2, 1 + 2 + 3, 1 + 2 + 3 + 4, etc. 1 is considered a triangular number even though it does not look much like a triangle when you draw it (see the smallest pentagon picture)! The magenta triangles show 1 + 2, 1 + 2 + 3, 1 + 2 + 3 + 4, 1 + 2 + 3 + 4 + 5, etc.
Total number of dots in each pentagon:
Pentagon 0: 1 (not shown)
Pentagon 1: 5
Pentagon 2: 12
Pentagon 3: 22
Pentagon 4: 35
The number of dots increases according the the pattern 1 , 1 + 4, 1 + 4 + 7 , 1 + 4 + 7 + 10, 1 + 4 + 7 + 10 + 13, etc., where the new number added increases by 3 each time. (Students can try to use the pictures to explain why this happens.)
The number of dots in pentagon n is the sum of the number of dots in the (n + 1)th triangle plus two times the number of dots in the nth triangle, where the triangles are numbered according to the pattern:
Triangle 1: 1
Triangle 2: 3
Triangle 3 6
Triangle 4: 10
Triangle 5: 15
A formula for the nth triangular number is
A formula for the nth pentagonal number is
Students may discover many different equivalent versions of these formulas.
Back to Creative Math Prompts Previous prompt for Later Grades Next prompt for Later Grades